前些天我在博客上分享了使用FPGA+AD9361进行DPSK调制的过程,相对于DPSK解调来说,DPSK调制过程比较简单。一个显而易见的问题是,作为发送端的AD9361与作为接收端的AD9361的本振频率必定存在偏差,使得AD9361接收到的基带数据像是被调制了一样。我在尝试分析本振频偏问题时,曾经使用信号源生成DPSK信号并由AD9361接收,故意将信号源的本振频率设定一点偏移,就可以发现AD9361接收到数据包络跟着变化,因此,如果想正确解调DPSK数据,就必须消除载波频偏。
事实上,接收端解调时如果残留频偏(或者相位偏差)较大时,系统的误码特性将出现平顶效应,此时无论信噪比增大多少,都不能使误码率显著降低。受到一篇论文的启发,我采用了一种特别简单有效的方法实现了DPSK解调的同时,消除了载波频偏,在此分享给各位读者。
原理分析
由AD9361接收,正交解调并AD采用后的n时刻基带数据可表示为
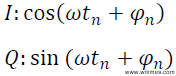
n-1时刻基带数据可表示为
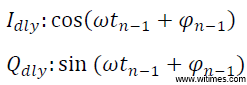
其中w是接收端与发射端的载波频率偏差,利用三角函数公式,有
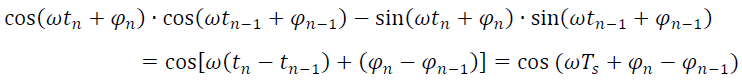
其中
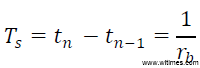
通常,wTs近似为0,所以这个运算得到的结果就是解调后的数据。
Matlab验证
首先使用Vivado的ila抓取AD9361 AD采样后的基带数据,如下图,从图中可以看出本来应该是恒包络的波形由于载波频偏的存在严重变形了,就像被AM调制了一样。

然后将ila抓取到的数据保存为csv格式,供Matlab使用。
在Matlab中将csv数据读入,匹配滤波,抽取之后进行频偏补偿,解调,我采用了三种方式:
- 改进型,即前文分析的方法
- FFT频偏补偿,对接收到的I路或者Q路基带信号进行FFT变换,得到载波频偏,再将其与原始I路、Q路基带数据相乘,相加,这种方式可以消除较大的频偏,如多普勒频移,但是会有残留的频偏及相偏,需要进一步使用Costas环纠正
- 无补偿
对于同样的基带数据,三种解调方式得到的波形分别如下:
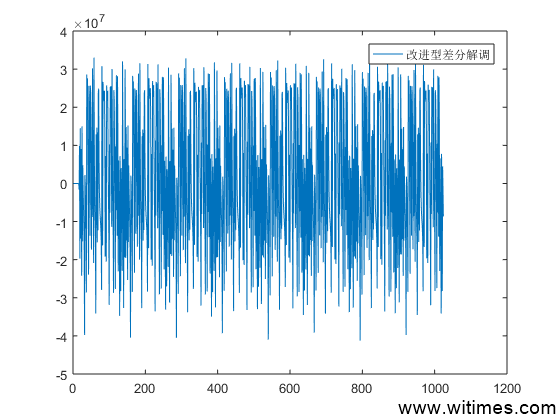
改进型,可以看出载波频偏已消除
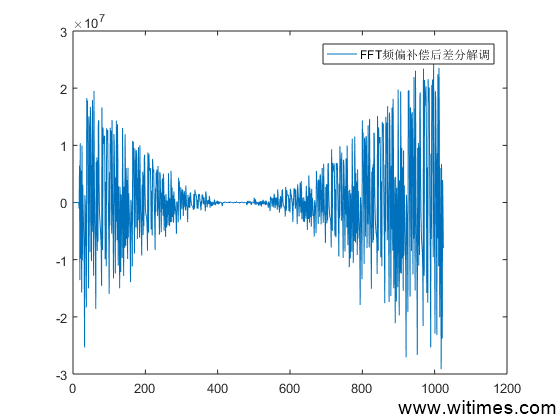
FFT频频补偿,可以看到仍有残留的频偏
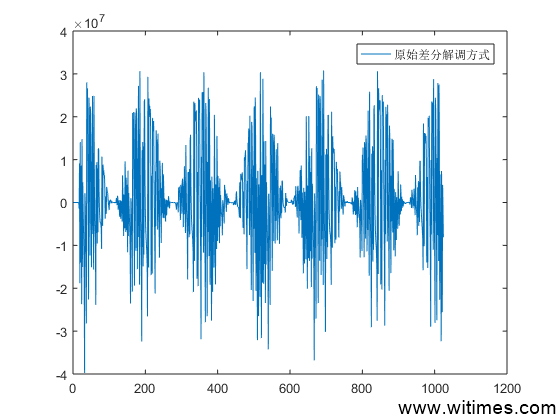
无补偿,可以看出这种情况最糟糕
在本例中,发送序列是已知的,所以可以轻易地构造出较长的发送序列并与解调后的数据做对比,得到误码率,其结果如下,可以看出,改进型DPSK解调的误码率为0。