什么是成型滤波
成型滤波就是通过对数字基带信号的处理把信号的频谱压缩在一定的带宽内。先看一张图,就是矩形脉冲信号的频谱,这张图是用别人的代码画出来的,比我的代码画的好,毕竟人家是专业的。
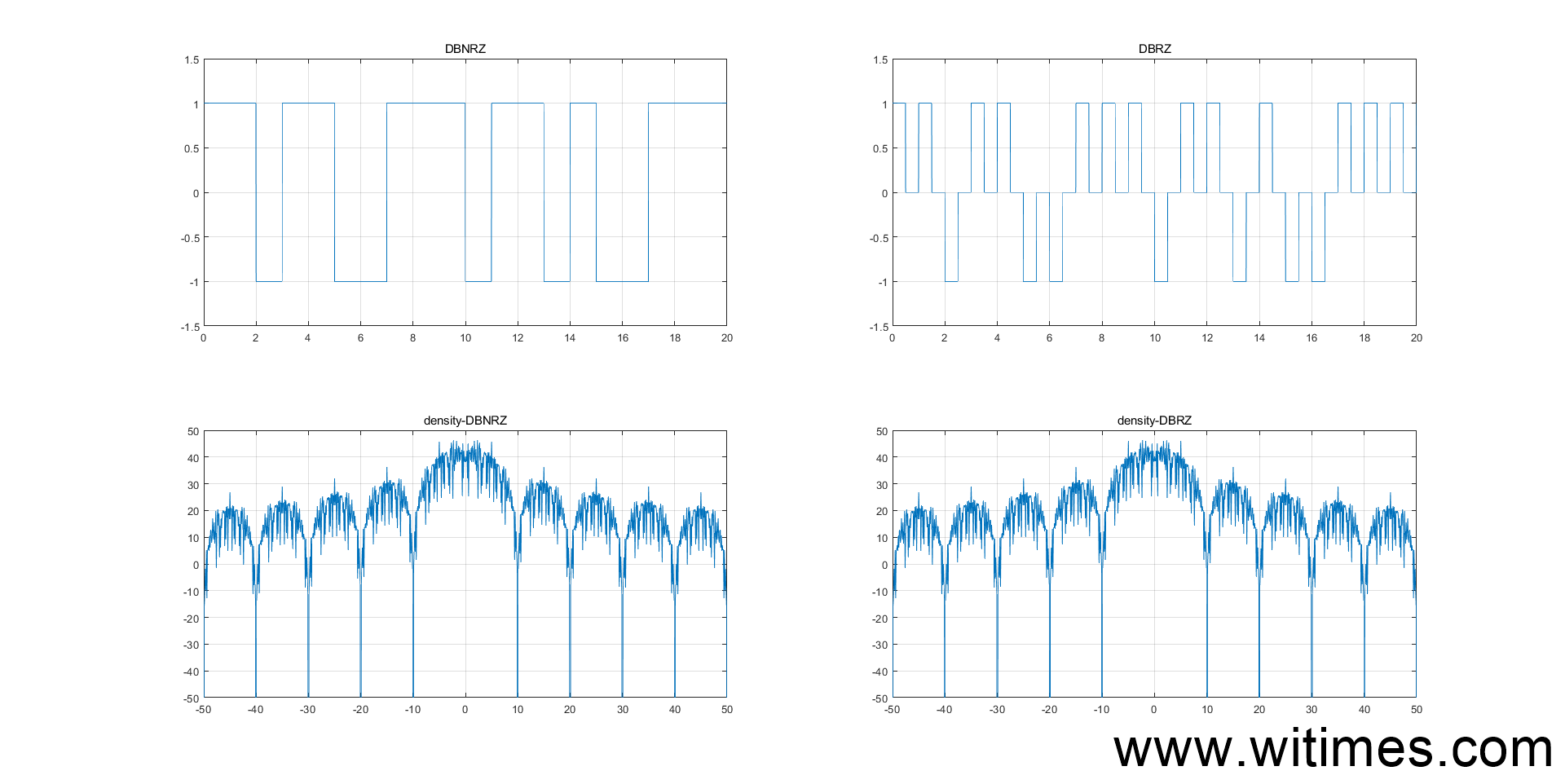
很明显,如果不对这个频谱做限制,那么它将会占用特别大的带宽,在实际的无线通信产品中,根本没有这种频谱的产品。用比较专业的一点的方式描述,成型滤波有两个作用:
(1)频谱压缩,限制信号带宽。在数字通信中基带信号是矩形脉冲,突变的上升沿和下降沿包含高频分量丰富,其频谱范围普遍比较宽(频谱是一个Sa函数)。为了有效利用信道,在信号传输之前,需要对信号进行频谱压缩。使其在消除码间串扰和达到最佳检测的前提下,大大提高频带利用率。信号带宽匹配信道带宽。
(2)改变传输信号的成形波形,可以减小抽样定时脉冲误差所带来的影响,即降低了码间干扰(ISI)。信号带限就会引入码间串扰(时域的离散化对应频域的周期化),会导致接收信号波形失真。但一般情况下,只需要在特定时刻的信号抽样值无失真,并不需要整个信号波形都无失真,而升余弦滤波器刚好就能对基带信号频谱进行带限,并且不影响信号在特定时刻的抽值
原文链接:https://blog.csdn.net/weixin_46136963/article/details/107981923
成型滤波器的原理
我在研究成型滤波这部分知识的时候花了大量时间,我无法给出教材上那么详细的资料,只能是按照我的个人理解和学习过程做简单总结,想要进一步学习的话,就得学习信号与系统与数字信号处理了。数字滤波器分为FIR(有限冲击响应)和IIR(无限冲击响应),其中FIR无反馈模块,IIR有反馈模块,可想而知,FIR的输出与之前的输出无关,IIR的输出与之前的输出是有关系的,还需要记住另一个结论,FIR具有线性相位。FIR滤波器具有很多结构,我画了一种最简单的形式,如下图。读者可能会觉得手动画图多此一举,其实我画图是为了加深理解,我还自己手动计算过滤波器的输出^_^。
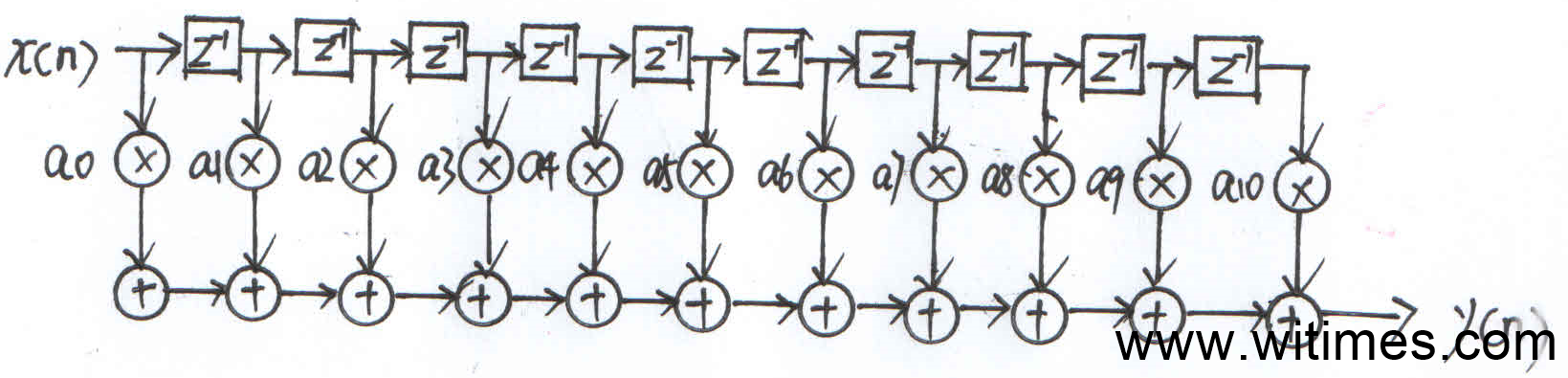
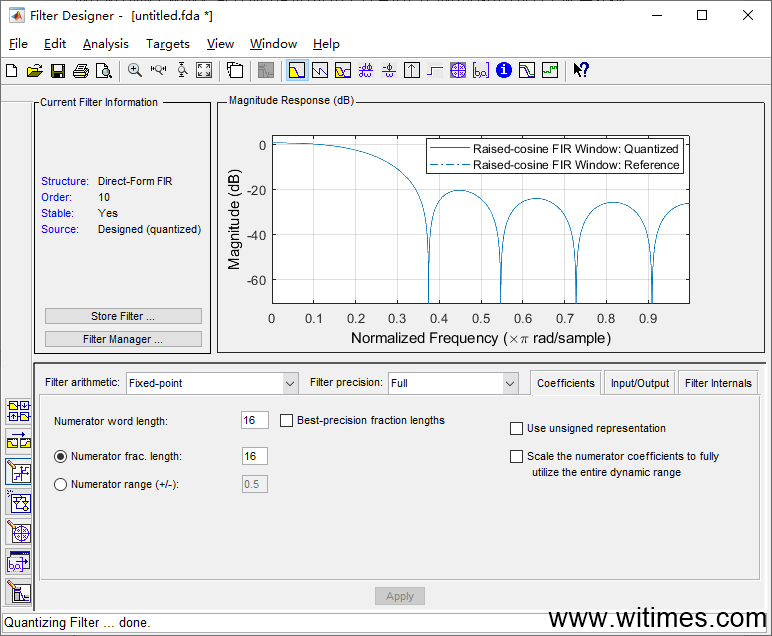
可以看出,这是一种延迟,相乘再相加的结构,实际上就是卷积和,其中x(n)是输入的数字序列,y(n)是输出的数字序列,a0-a10称为滤波器的系数,卷积的计算过程就是:换元、翻转、移位、相乘求和,一边卷动,一边求和,很形象。为了验证这个想法,我们用Matlab设计一个升余弦滤波器,如下图。
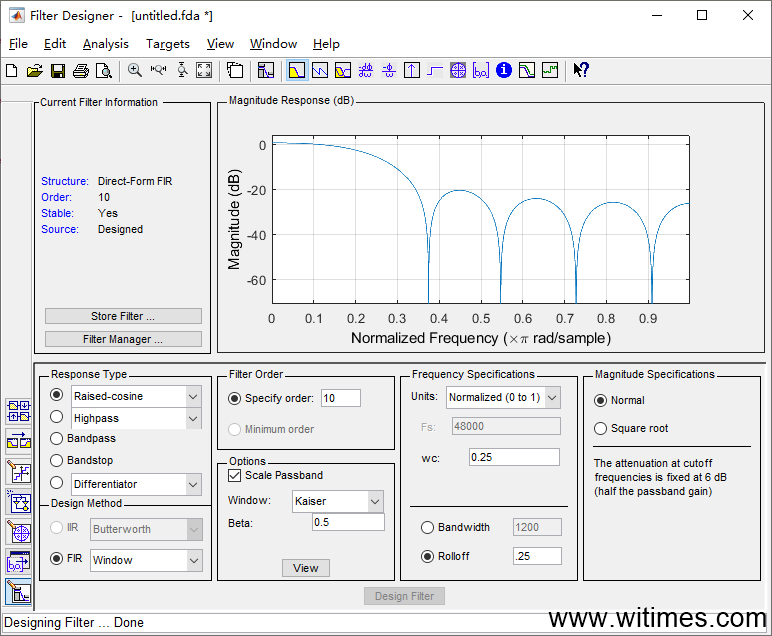
量化成16位
并保存量化后的系数-2529,0,4654,10179,14661,16384,14661,10179, 4654,0,-2529
假定输入序列x(n)是[1,-1,-1,-1,-1,-1,-1,-1,1],可以算出滤波器的输出
y(0)=a0*x(0) =-2529
y(1)=a0*x(1)+a1*x(0)=2529
y(2)=a0*x(2)+a1*x(1)+a2*x(0)=7183
y(3)=a0*x(3)+a1*x(2)+a2*x(1)+a3*x(0)=8054
y(4)=……=2357
y(5)=……=-10581
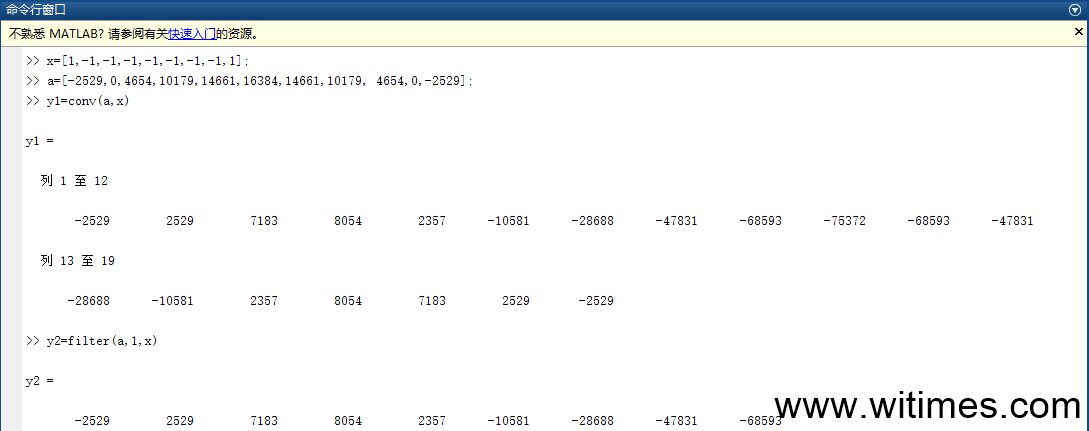
好,这是手动计算的结果,我们再来看看Matlab函数的输出结果,如下图。
其中y1是卷积运算的结果,y2是使用Matlab的filter函数滤波后的结果,可见,y2与y1的前几个输出值是完全匹配的。以上过程说明数字滤波器的输出的确就是输入序列与滤波器系数卷积的结果。还有一个问题,为什么把原始数字序列与滤波器系数卷积后,频谱特性就改变了呢?我自己的理解是,当前的输出是之前的多个输入值乘系数相加后的结果,可以起到对输入信号进行平滑处理,既然信号变得平滑了,信号突变也就没那么厉害了,信号的频率成分必定减少,频谱自然被压缩。从数学上看,数字滤波器的输入与输出可以表达为差分方程,这个差分方程的频率响应呈现出低通、高通、带通等形式,奥本海姆的《信号与系统》写得很好,感兴趣的读者可以看看。
成型滤波器在FPGA上的实现
(1) 首先生成20000个1 -1的随机序列,并保存在rand_data.txt文件中,Matlab代码如下:
clear;clc;
N=20000;
s=randi([0 1],N,1);
s1=2*s-1;
fid=fopen('D:\Temp\matlab\rand_data.txt','w');
fprintf(fid,'%d\r\n',s1);fclose(fid);
(2) 生成一个128阶,滚降系数是0.25的,归一化截止频率0.25的平方根升余弦滚降滤波器,并量化为16位整数,保存为coe格式,供Vivado使用。Matlab代码如下:
clear;clc;
span=32; %符号跨度
sps=4; %每个符号的点采样数
%使用rcosdesign得到滤波器系数
h=rcosdesign(0.25, span, sps, 'sqrt');
%得到的系数通带增益为6dB,暂不清楚原因,除2后正常
h2=h/2;
figure (1);
freqz(h2,1,1024);
%将系数放大并取整
coe_int=round((h/max(abs(h)))*(2^15-1));
freqz(coe_int,1,1024);
format long;
%将系数量化为15位小数
coe_frac=coe_int/2^15;
figure (2);
freqz(coe_frac,1,1024);
fid=fopen('D:\Temp\matlab\coe_frac.coe','w');
fprintf(fid,'Radix = 10;\r\n');
fprintf(fid,'CoefData =\r\n');
fprintf(fid,'%16.15f,\r\n',coe_frac);fprintf(fid,';');fclose(fid);
fid=fopen('D:\Temp\matlab\coe_int.coe','w');
fprintf(fid,'Radix = 10;\r\n');
fprintf(fid,'CoefData =\r\n');
fprintf(fid,'%d,\r\n',coe_int);fprintf(fid,';');fclose(fid);
fid=fopen('D:\Temp\matlab\coe_int.txt','w');
fprintf(fid,'%d ',coe_int);fclose(fid);
频率响应如下图
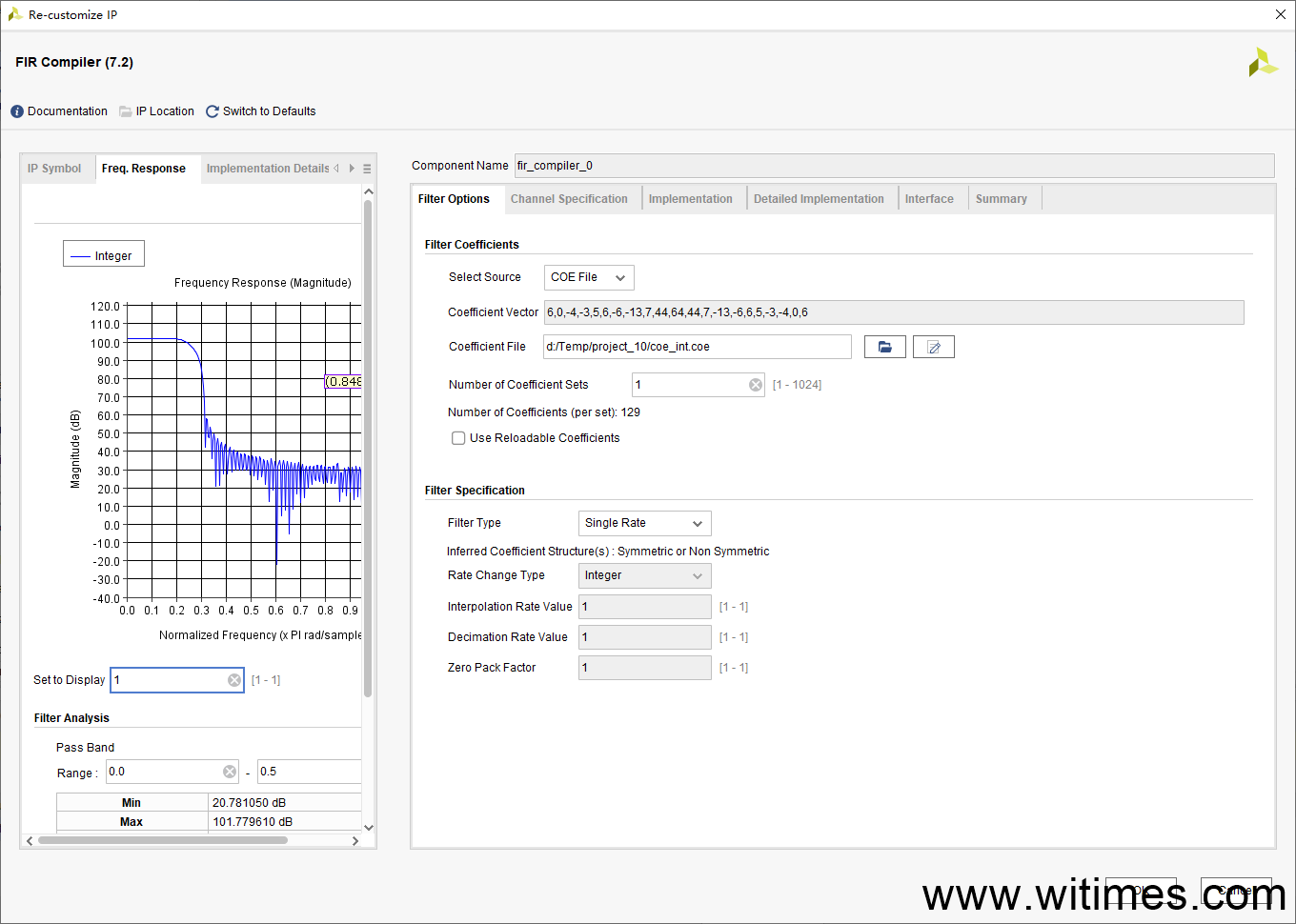
(3) 在Vivado中使用FIR IP核,加载coe_int.coe文件,并作如下配置
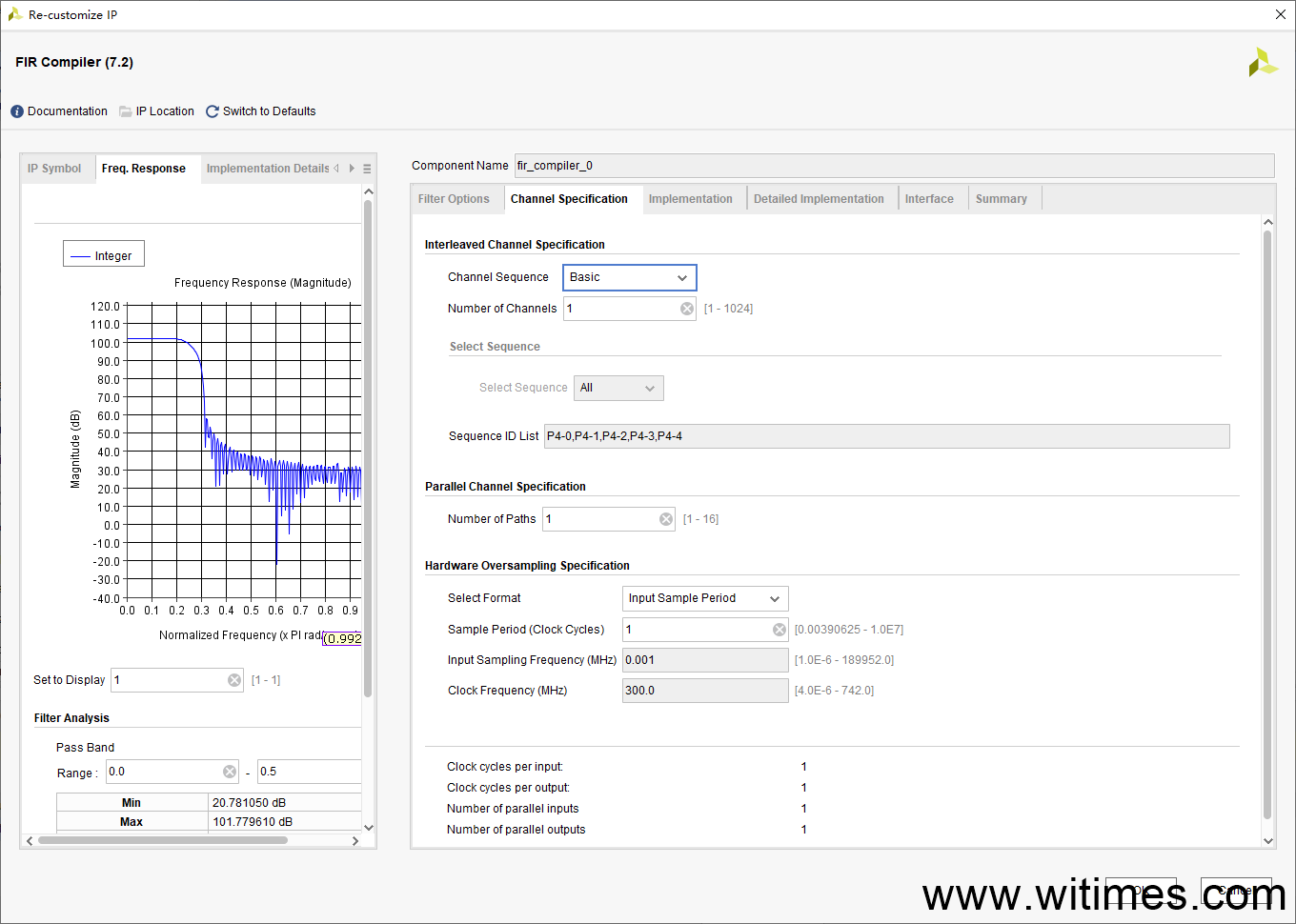
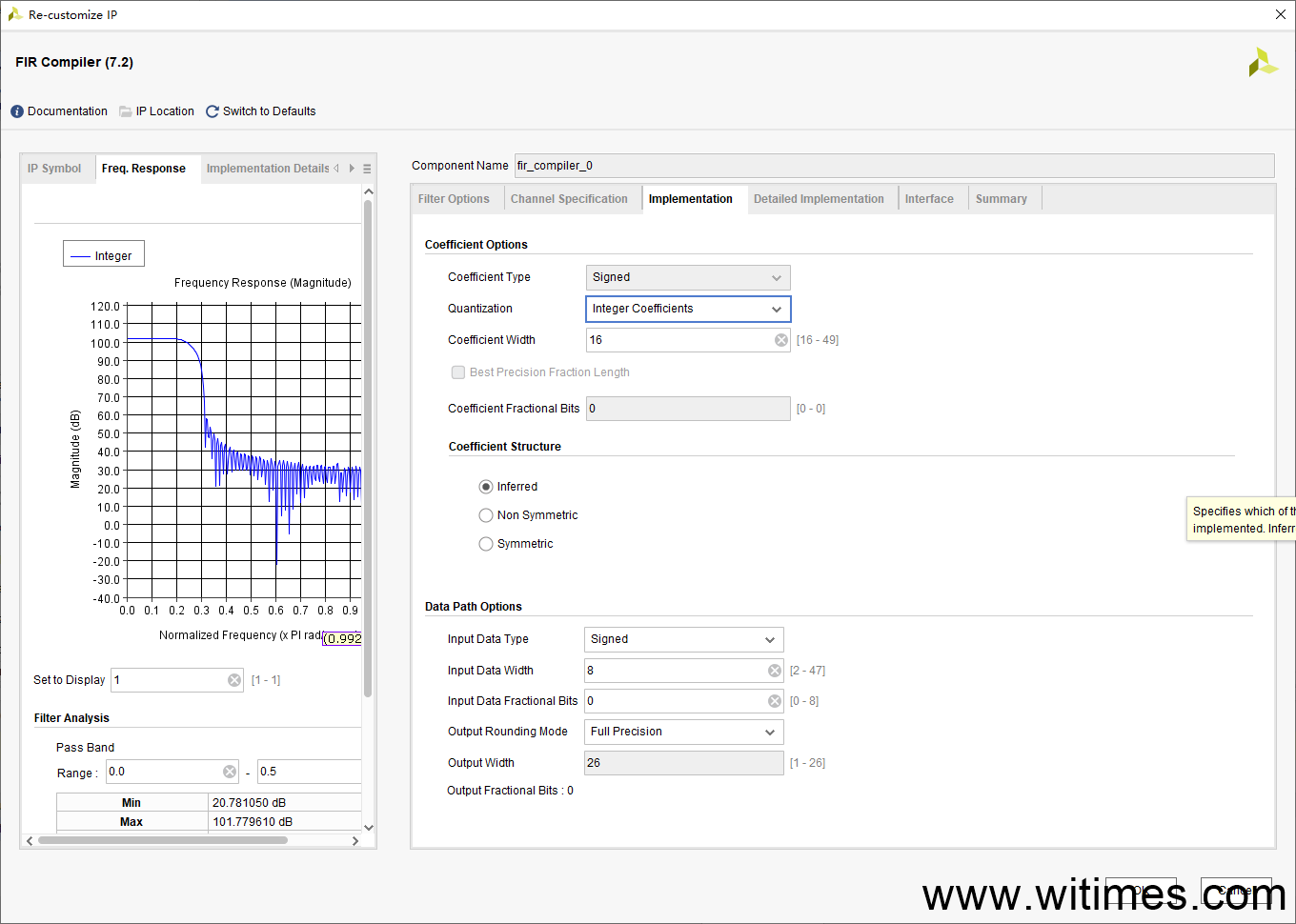
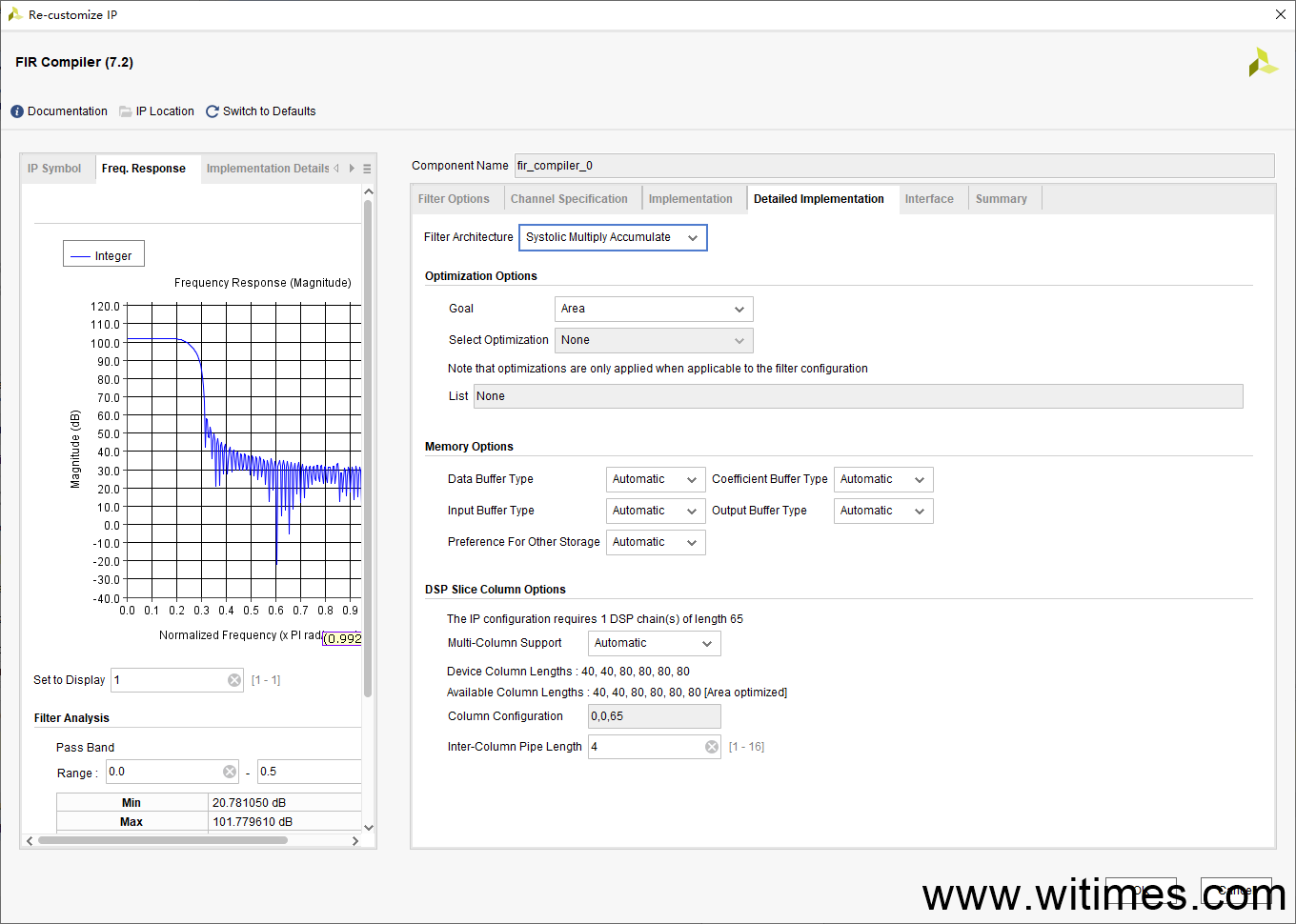
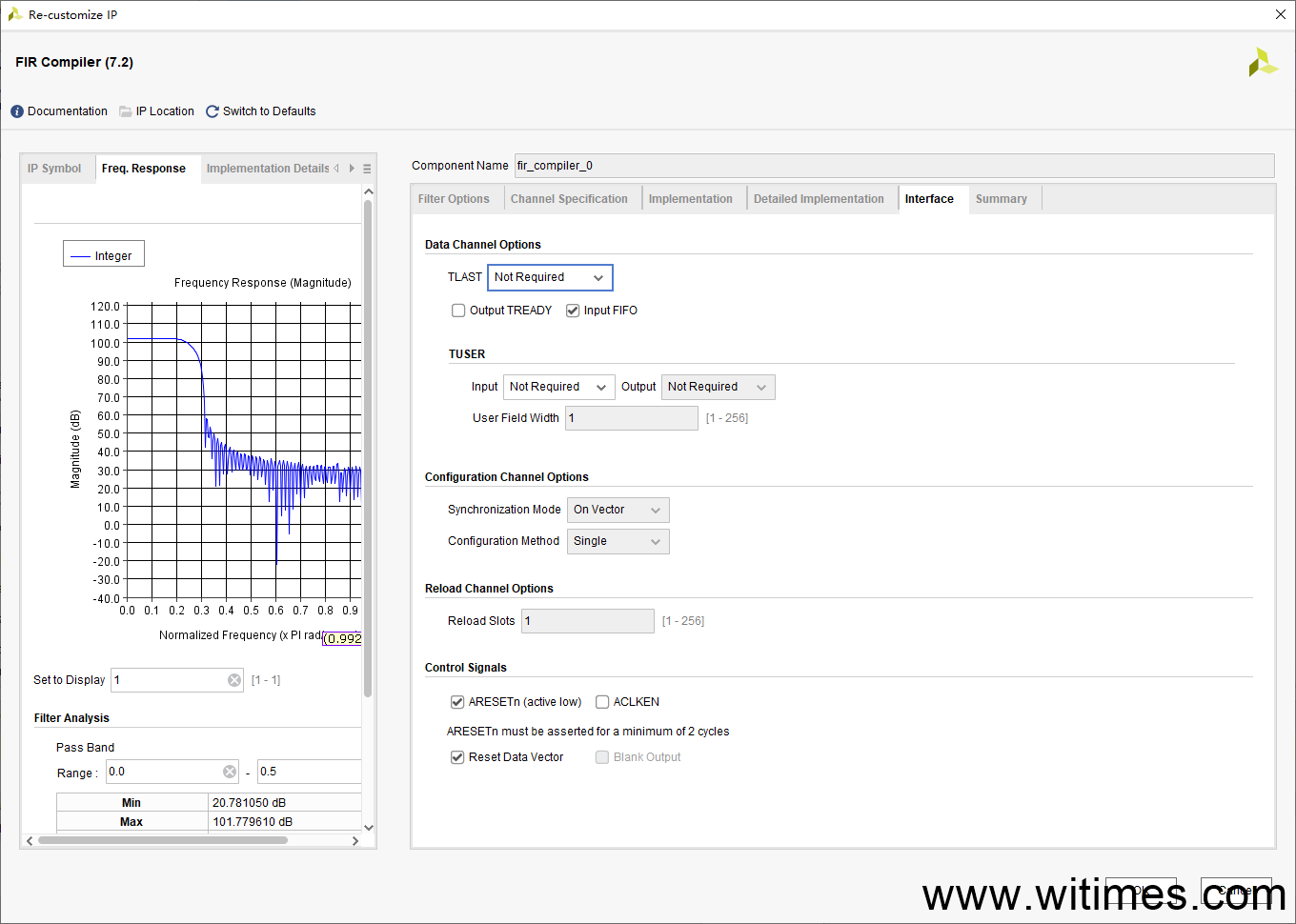
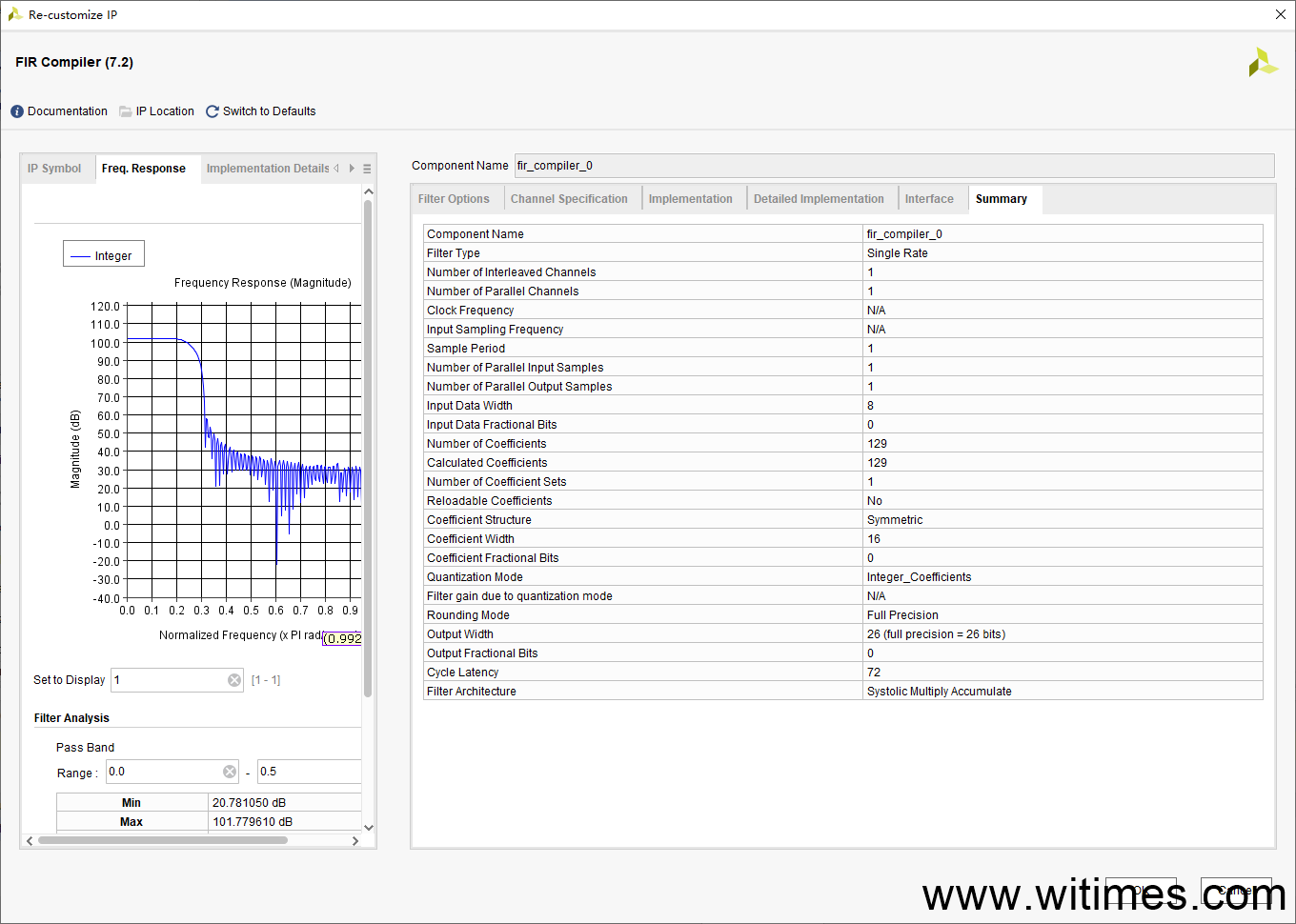
(4) 编写testbench,读入第(1)步生成的rand_data.txt,并将FIR滤波后的结果保存在filt_data.txt中,部分代码如下
integer fid_in;
initial
begin
fid_in = $fopen("D:/Temp/matlab/rand_data.txt","r");
end
always@(posedge clk_1m)
begin
if(!rst)
begin
din <= 8'd0;
s_data_tvalid <= 1'b0;
end
else if(s_data_tready)
begin
$fscanf(fid_in,"%d",din);
s_data_tvalid <= 1'b1;
end
end
integer fid_out;
initial
begin
fid_out = $fopen("D:/Temp/matlab/filt_data.txt","w");
end
always@(posedge clk_4m)
begin
if(m_data_tvalid)
begin
$fwrite(fid_out,"%d\n",dout);
end
end
(5) 配置Vivado使用Modelsim仿真并运行,得到filt_data.txt。
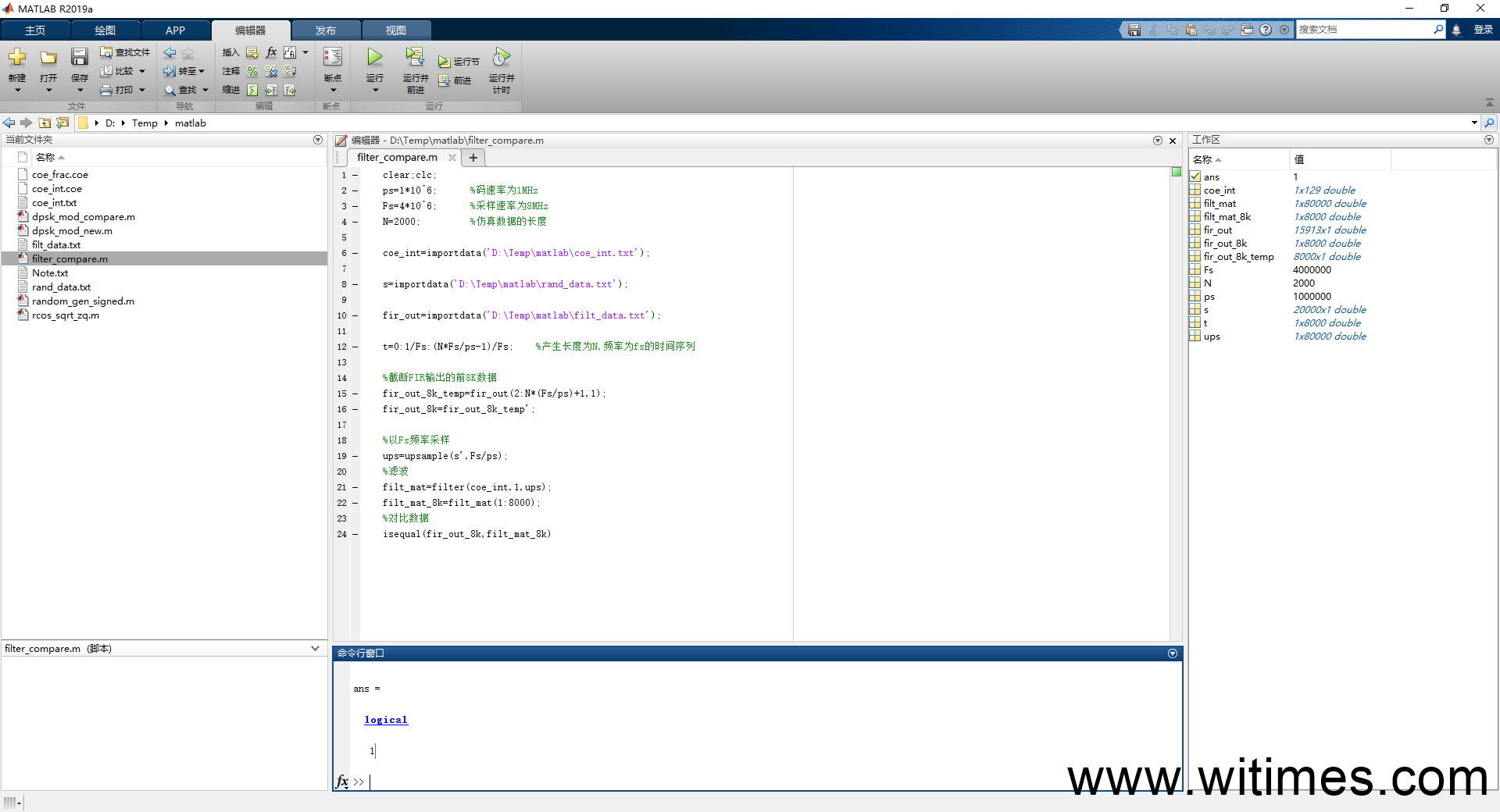
(6) 使用对比filt_data.txt与Matlab使用filter函数得到的结果是否一致,代码如下
clear;clc;
ps=1*10^6; %码速率为1MHz
Fs=4*10^6; %采样速率为8MHz
N=2000; %仿真数据的长度
coe_int=importdata('D:\Temp\matlab\coe_int.txt');
s=importdata('D:\Temp\matlab\rand_data.txt');
fir_out=importdata('D:\Temp\matlab\filt_data.txt');
t=0:1/Fs:(N*Fs/ps-1)/Fs; %产生长度为N,频率为fs的时间序列
%截断FIR输出的前8K数据
fir_out_8k_temp=fir_out(2:N*(Fs/ps)+1,1);
fir_out_8k=fir_out_8k_temp';
%以Fs频率采样
ups=upsample(s',Fs/ps);
%滤波
filt_mat=filter(coe_int,1,ups);
filt_mat_8k=filt_mat(1:8000);
%对比数据
isequal(fir_out_8k,filt_mat_8k)
对比结果如下
可见,FIR滤波器与Matlab filter函数的输出结果完全一致。